TTC Video – Understanding Multi-variable Calculus
$320 Original price was: $320.$59Current price is: $59.
Shopping Instructions:
- DISCOUNT 15% : SHOP15
- Product Delivery: Within 1 – 12 hours after purchase.
Understanding Multivariable Calculus: Problems, Solutions, and Tips, taught by award-winning Professor Bruce H. Edwards of the University of Florida, brings the basic concepts of calculus together in a much deeper and more powerful way.
File size: 13.03GB
TTC Video – Understanding Multi-variable Calculus
Whether calculating the volume of odd-shaped objects, predicting the outcome of a large number of trials in statistics, or even predicting the weather, we depend in myriad ways on calculus in three dimensions. Once we grasp the fundamentals of multivariable calculus, we see how these concepts unfold into new laws, entire new fields of physics, and new ways of approaching once-impossible problems.
With multivariable calculus, we ge
- new tools for optimization, taking into account as many variables as needed;
- vector fields that give us a peek into the workings of fluids, from hydraulic pistons to ocean currents and the weather;
- new coordinate systems that enable us to solve integrals whose solutions in Cartesian coordinates may be difficult to work with; and
- mathematical definitions of planes and surfaces in space, from which entire fields of mathematics such as topology and differential geometry arise.
Understanding Multivariable Calculus: Problems, Solutions, and Tips, taught by award-winning Professor Bruce H. Edwards of the University of Florida, brings the basic concepts of calculus together in a much deeper and more powerful way. This course is the next step for students and professionals to expand their knowledge for work or study in many quantitative fields, as well as an eye-opening intellectual exercise for teachers, retired professionals, and anyone else who wants to understand the amazing applications of 3-D calculus.
Designed for anyone familiar with basic calculus, Understanding Multivariable Calculus follows, but does not essentially require knowledge of, Calculus II. The few topics introduced in Calculus II that do carry over, such as vector calculus, are here briefly reintroduced, but with a new emphasis on three dimensions.
Your main focus throughout the 36 comprehensive lectures is on deepening and generalizing fundamental tools of integration and differentiation to functions of more than one variable. Under the expert guidance of Professor Edwards, you’ll embark on an exhilarating journey through the concepts of multivariable calculus, enlivened with real-world examples and beautiful animated graphics that lift calculus out of the textbook and into our three-dimensional world.
A New Look at Old Problems
How do you integrate over a region of the xy plane that can’t be defined by just one standard y = f(x) function? Multivariable calculus is full of hidden surprises, containing the answers to many such questions. In Understanding Multivariable Calculus, Professor Edwards unveils powerful new tools in every lecture to solve old problems in a few steps, turn impossible integrals into simple ones, and yield exact answers where even calculators can only approximate.
With these new tools, you will be able to
- integrate volumes and surface areas directly with double and triple integrals;
- define easily differentiable parametric equations for a function using vectors; and
- utilize polar, cylindrical, and spherical coordinates to evaluate double and triple integrals whose solutions are difficult in standard Cartesian coordinates.
Professor Edwards leads you through these new techniques with a clarity and enthusiasm for the subject that make even the most challenging material accessible and enjoyable. With graphics animated with state-of-the-art software that brings three-dimensional surfaces and volumes to life, as well as an accompanying illustrated workbook, this course will provide anyone who is intrigued about math a chance to better understand the full potential of one of the crowning mathematical achievements of humankind.
About Your Professor
Dr. Bruce H. Edwards is Professor of Mathematics at the University of Florida. He earned his Ph.D. in Mathematics from Dartmouth College. He has been honored with numerous Teacher of the Year awards as well as awards for his work in mathematics education for the state of Florida.
-
1A Visual Introduction to 3-D Calculus
-
2Functions of Several Variables
-
3Limits, Continuity, and Partial Derivatives
-
4Partial Derivatives—One Variable at a Time
-
5Total Differentials and Chain Rules
-
6Extrema of Functions of Two Variables
-
7Applications to Optimization Problems
-
8Linear Models and Least Squares Regression
-
9Vectors and the Dot Product in Space
-
10The Cross Product of Two Vectors in Space
-
11Lines and Planes in Space
-
12Curved Surfaces in Space
-
13Vector-Valued Functions in Space
-
14Kepler’s Laws—The Calculus of Orbits
-
15Directional Derivatives and Gradients
-
16Tangent Planes and Normal Vectors to a Surface
-
17Lagrange Multipliers—Constrained Optimization
-
18Applications of Lagrange Multipliers
-
19Iterated integrals and Area in the Plane
-
20Double Integrals and VolumeIn taking the next step in learning to integrate multivariable functions, you’ll find that the double integral has many of the same properties as its one-dimensional counterpart. Evaluate these integrals over a region R bounded by variable constraints, and extrapolate the single variable formula for the average value of a function to multiple variables.
-
21Double Integrals in Polar Coordinates
-
22Centers of Mass for Variable Density
-
23Surface Area of a Solid
-
24Triple Integrals and Applications
-
25Triple Integrals in Cylindrical Coordinates
-
26Triple Integrals in Spherical Coordinates
-
27Vector Fields—Velocity, Gravity, Electricity
-
28Curl, Divergence, Line Integrals
-
29More Line Integrals and Work by a Force Field
-
30Fundamental Theorem of Line Integrals
-
31Green’s Theorem—Boundaries and Regions
-
32Applications of Green’s Theorem
-
33Parametric Surfaces in Space
-
34Surface Integrals and Flux Integrals
-
35Divergence Theorem—Boundaries and Solids
-
36Stokes’s Theorem and Maxwell’s Equations
Related products
Personal Development
Tony Robbins – New Money Masters Elite + Bonuses [Complete Version]
Personal Development
ThinkEatLift – Radu Antoniu. Andrei Antoniu – Unstoppable Discipline
Personal Development
Personal Development
Tarek Bibi – The Ascension Program For Lightworkers & Empaths
Personal Development
Personal Development
Bob Proctor – The secret to Wealth – Mind & Money Strategies
Personal Development



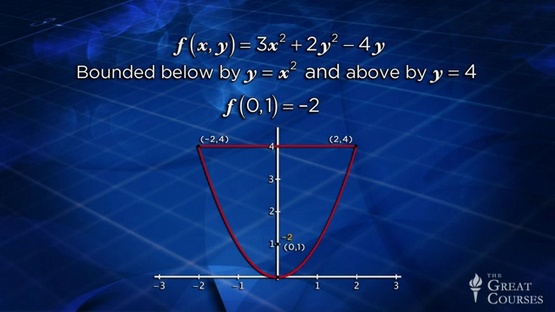

![Tony Robbins – New Money Masters Elite + Bonuses [complete Version]](https://copicourse.com/wp-content/uploads/2021/08/tony-robbins-new-money-masters-elite-bonuses-complete-version-300x400.jpg)






